Ecuaciones de Maxwell
¿Qué son las ecuaciones de Maxwell?
Las ecuaciones de Maxwell comprenden cuatro principios y leyes de los fenómenos eléctricos, magnéticos y ópticos. Constituyen los cálculos más fundamentales de la electrodinámica. Las ecuaciones de Maxwell fueron formuladas por el físico escocés James Clerk Maxwell entre 1861 y 1864. Las fórmulas definen cómo se relacionan los campos eléctricos y magnéticos. Además, las teorías de Maxwell también describen la relación entre las cargas eléctricas y la corriente eléctrica en determinadas condiciones.
Hoy en día, las ecuaciones de Maxwell constituyen la base teórica de la óptica, la electrostática y la ingeniería eléctrica. Son un complejo sistema de ecuaciones diferenciales parciales lineales de primer orden. En principio, los cálculos describen el comportamiento de las ondas electromagnéticas, por lo que siguen teniendo gran importancia en la física actual.
Las cuatro ecuaciones de Maxwell y sus funciones
Maxwell utilizó un total de cuatro fórmulas y sus derivadas, así como diversas derivadas para sus ecuaciones, que hoy llevan su nombre. El físico combinó en un solo tratado las leyes conocidas en la época y añadió a las ecuaciones la corriente de desplazamiento. Explicado de forma sencilla, el contenido físico de las ecuaciones de Maxwell puede expresarse bien en las conocidas leyes del electromagnetismo:
Ecuación de Maxwell o ley de Coulomb: la primera ecuación describe que los campos eléctricos D son causados por cargas eléctricas (densidad de carga ρ). El conjunto de líneas de campo del campo eléctrico E se caracteriza por la divergencia de un campo (∇×E).
Ecuación de Maxwell: describe que todas las líneas de campo del campo magnético B son siempre autocontenidas y que no existen monopolos magnéticos. Las líneas de campo no discurren como un vector, sino en círculo. Además, la dirección de las líneas de campo está definida con precisión: Siempre describen un círculo desde el polo norte hasta el polo sur de un imán:
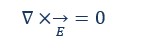
Ecuación de Maxwell: los campos eléctricos y las tensiones se generan al cambiar los campos magnéticos. Esto se conoce como inducción electromagnética, causada por corrientes de desplazamiento. B representa la densidad de flujo magnético.
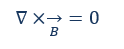
- Ecuación de Maxwell o ley de flujo (ley de Ampère): muestra en qué medida los campos eléctricos variables en el tiempo generan campos magnéticos. μ0 describe la permeabilidad magnética del vacío o aproximadamente la del espacio aéreo. j son las corrientes del campo magnético.
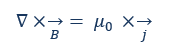
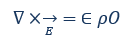
En esta forma, las ecuaciones de Maxwell se refieren siempre al entorno del vacío. Sin embargo, en sus consideraciones posteriores tiene en cuenta la materia a partir de parámetros específicos de los materiales. Esto es esencial para la descripción y propagación de los campos eléctricos y magnéticos. Las ecuaciones de Maxwell tienen una forma diferencial y otra integral.
¿Por qué las ecuaciones de Maxwell pusieron en tela de juicio el principio de la relatividad?
La teoría especial de la relatividad (TER) describe el movimiento de campos y cuerpos en el espacio y el tiempo. Fue desarrollada por Albert Einstein como una extensión del principio galileano de la relatividad. La TER estipula que todas las leyes de la física tienen la misma forma en todos los marcos de referencia inerciales. Esto también se aplica al campo del electromagnetismo, que se describe mediante las ecuaciones de Maxwell.
La TER describe en sus rasgos básicos que las longitudes y duraciones dependen individualmente del estado de movimiento de un observador. Por lo tanto, no existen ni el espacio ni el tiempo absolutos. Estos supuestos se expresan en el tensor de magnitudes matemáticas. Ésta se basa en el espacio tridimensional. Las ecuaciones de Maxwell también pueden representarse como un tensor de tensiones. Esto se conoce como tensor de Maxwell o tensor de intensidad de campo electromagnético.
Las ecuaciones se incluyen en la teoría especial de la relatividad y describen las fuerzas que actúan sobre un cuerpo sometido a aceleración. Los científicos han discrepado durante mucho tiempo sobre el carácter absoluto del espacio y el tiempo. Por ello, durante años la teoría de la relatividad no pudo demostrarse plenamente. Posteriormente, Einstein rechazó estas dudas con el paso de la transformación galileana a la de Lorentz. Por eso, las ecuaciones de Maxwell siguen ocupando hoy un lugar firme en la teoría de la relatividad.
 Miles de productos en stock
Miles de productos en stock