Miles de productos en stock
Densidad de flujo magnético
La densidad de flujo magnético se define como la densidad de las líneas de campo. Como el llamado campo B, es indirectamente una medida para indicar la intensidad de un campo magnético. El término campo B es deliberado: no es el campo magnético real, aunque los dos términos se utilicen a veces indistintamente en la literatura.
Cálculo de la densidad de flujo magnético
Mientras que la densidad de flujo magnético se describe con la letra B según la definición, la letra para el campo magnético es H. Se aplica la siguiente relación con las denominadas constantes de permeabilidad μ0 (para el vacío) y μ (para materiales adicionales):
La constante de permeabilidad puede variar en función del tipo de material:
- siempre que no se trate de un material ferromagnético, la constante de permeabilidad específica del material μ se sitúa en torno a 1.
- con materiales ferromagnéticos, este valor puede llegar a veces hasta 100.000.
- Si, por el contrario, se trata de un superconductor μ = 0.
El producto de las dos constantes de permeabilidad y el campo magnético H da, por tanto, la densidad de flujo magnético B por definición. Se mide en la unidad Tesla (T).
Antecedentes
Muchas personas no están muy familiarizadas con la fórmula de la densidad de flujo magnético mencionada anteriormente. La explicación ilustrativa de los antecedentes físicos debería servir de ayuda: Alrededor de un conductor por el que circula corriente se forma un campo magnético. Este ejerce fuerzas sobre el cobalto, el níquel, el hierro u otros materiales ferromagnéticos cercanos. A su vez, la densidad de flujo magnético B indica la intensidad real de este campo magnético. A veces también se denomina inducción magnética. B describe la densidad del flujo magnético a través de una superficie. Existen numerosas fórmulas para realizar este cálculo.
Densidad de flujo magnético frente a flujo magnético: ¿hay alguna diferencia?
La densidad del flujo magnético que atraviesa una superficie imaginaria es, por tanto, el flujo magnético. Es útil imaginar una imagen de las líneas de campo magnético entre dos polos. La densidad de las líneas de campo en una sección transversal es efectivamente la densidad de flujo magnético.
De acuerdo con las ecuaciones de Maxwell -una conocida ley física de la electrodinámica-, las líneas de campo no pueden detenerse. Por tanto, la densidad de flujo de un imán continúa en su espacio exterior. El flujo magnético propiamente dicho tiene el símbolo Φ y básicamente denota la totalidad de todas las líneas de campo magnético. El flujo magnético es, por tanto, el producto de una determinada área A y la densidad de flujo magnético B. El área debe ser perpendicular al flujo.
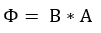
Las cargas en movimiento, es decir, las corrientes, generan un flujo magnético. Éste no tiene principio ni fin, ya que las corrientes sólo crean líneas de campo cerradas. Desde el punto de vista físico, esto significa que no hay fuentes ni sumideros de flujo magnético o densidad de flujo magnético. Este hecho es la razón por la que un imán siempre está formado por dos polos: Un polo sur y un polo norte.
Las ecuaciones de Maxwell de la electrodinámica expresan este hecho matemáticamente. Es importante comprender que los imanes permanentes también se basan en este comportamiento con respecto a la densidad de flujo magnético: en ellos se forman corrientes circulares microscópicas con una corriente I, causadas por los movimientos de los electrones en el material. Son las responsables del flujo magnético o campo magnético. La corriente circular crea un denominado momento magnético con el polo sur por debajo del bucle conductor y el polo norte por encima de este bucle conductor. Si se invirtiera el sentido de la corriente, los polos se invertirían.
Desde un punto de vista físico, el flujo magnético se define por el efecto inductivo que ejerce sobre una espira. Si se coloca un bucle conductor de superficie conocida en un campo magnético, se induce una sobretensión. El flujo magnético es igual a la integral de tiempo sobre esta sobretensi:
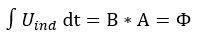
El flujo magnético se mide utilizando este bucle conductor y la tensión inducida en él. Sin embargo, éste ya no es un método habitual. La denominada sonda Hall es mucho más precisa. Si la densidad de flujo magnético atraviesa una superficie curva, el flujo magnético debe definirse como la integral sobre la normal de superficie de la densidad de flujo vectorial: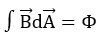 
Las líneas de campo que entran a través de una superficie cerrada -por ejemplo, la superficie de una esfera- también deben volver a salir de ella. Ésta es la naturaleza de las líneas de campo cerradas: matemáticamente, esto se manifiesta en el hecho de que el flujo magnético a través de superficies cerradas es siempre cero. Por consiguiente, no hay fuentes ni sumideros en la densidad de flujo magnético. 
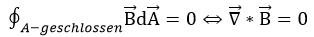Equivalente a esto es el enunciado de una de las cuatro ecuaciones de Maxwell sobre la llamada libertad de divergencia de la densidad de flujo magnético.